Introduction: Mathematical Foundations

Mathematics is a universal language that provides a systematic way to understand and describe the world. One of the most intriguing aspects of mathematics is how it can manipulate seemingly simple expressions into more complex forms. A prime example is the equation:

This equation, though appearing simple, encapsulates the deep relationship between exponential and logarithmic functions. Understanding this equation requires a firm grasp of exponential and logarithmic functions and their inherent properties. This article will delve deeply into the nature of this equation, exploring its derivation, properties, and practical applications.

Exponential Functions: Essential Concepts

Defining Exponential Functions

An exponential function is any mathematical expression in which a constant base is raised to a variable exponent. In the most common form:

Where:

• a is a constant and a>0.
• x is the variable exponent.

However, when a = e (Euler’s number, approximately 2.71828), the function becomes a natural exponential function:

This special form is central to studying continuous growth and decay processes, such as population growth, compound interest, and radioactive decay.

Properties of Exponential Functions

Logarithmic Functions: Inverse Mechanisms

Defining Logarithmic Functions

A logarithmic function is the inverse of an exponential function. For any base aaa, the logarithmic function is defined as:

These properties are critical in transforming and solving logarithmic equations.

Why It Is Valid

The equation is valid because the exponential and logarithmic functions are inverses. This is derived as follows:

1. Start with the definition: ln⁡x is the power to which e must be raised to get x.
2. Therefore, e^lnx directly translates to x.
3. This relationship is true for all x>0 because the natural logarithm ln⁡x is only defined for positive values.

Practical Example

Everyday Applications: Where It Matters

Financial Growth: Compound Interest

In finance, compound interest is closely linked to exponential functions. The general formula is:

Where:

• A is the final amount.
• P is the principal.
• r is the interest rate.
• t is the time in years.

By manipulating this formula using e^lnx, we can derive the continuous growth model, emphasising the importance of exponential relationships.

Population Dynamics

Population growth often follows an exponential model:

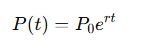
Here, P0 is the initial population, r is the growth rate, and t is time. The equation x=e^lnx is a fundamental identity allowing easy manipulation and understanding of this model.

Mathematical Properties: Further Exploration

Solving Complex Equations: Practical Usage

Example Problem

Explanation

This contradiction demonstrates that any manipulation away from the identity x=e^lnx can lead to inconsistencies, emphasising its unique truth.

Real-World Interpretation: Conceptual Insight

Data Science: Logarithmic Scaling

Data scientists often use logarithmic scaling to transform data, especially when handling skewed distributions. The transformation xlnx is a standard technique, and e^lnx ensures that transformed values can revert to their original scale.

Engineering: Signal Processing

In signal processing, logarithmic scales measure sound intensity (decibels), where relationships like x=e^lnx ensure consistent conversion between linear and logarithmic measures.

Conclusion: Profound Simplicity

The equation x=e^lnx is a profound yet straightforward identity that embodies the interplay between exponential and logarithmic functions. Understanding this relationship is crucial in calculus, financial modelling, data science, and engineering applications. This identity is a fundamental tool for transforming, analysing, and solving complex mathematical problems, providing a bridge between two of the most important mathematical functions.

Practice Exercises: Mastering x=e^lnx

To ensure a thorough understanding of the identity x=e^lnx, this section presents a variety of exercises. These problems range from basic applications to more complex manipulations. Each problem is followed by a detailed solution to enhance comprehension.

Exercise Set: Testing Your Understanding

Exercise 1: Basic Verification

Verify the identity x=e^lnx for the following values of x:

• x=2
• x=7
• x=0.5

Exercise 2: Solving for x

This is a contradiction. Therefore, there are no solutions for this equation.

Solution:

Solution:

Exercise 6: Functional Equation

Solution:

Exercise 7: Logarithmic Scaling

Solution:

Read Also: Comprehensive Guide: Understanding Circle Area.