Introduction
Integration is a fundamental concept in calculus and mathematics that deals with accumulating quantities and the area under curves. It is the inverse differentiation process and is critical in various fields, including physics, engineering, economics, and biology.
In simple terms, integration helps to determine the total effect when we know the rate of change.
1. Basic Concept of Integration
Integration in mathematics refers to finding the integral of a function. An integral represents the area under a curve or the accumulated quantity over an interval.
There are two main types of integrals:
- Definite Integrals – Represent the accumulation over a specific interval [a,b].
- Indefinite Integrals – Represent a family of functions and include an arbitrary constant C.
Notation
- Indefinite Integral:
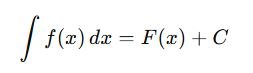
where F′(x)=f(x), and C is the constant.
- Definite Integral:
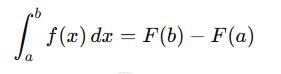
This gives a numeric value representing the area under the curve from a to b.
2. Properties of Integration
Understanding the properties of integrals simplifies complex problems:
Linearity Property
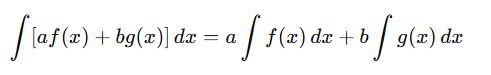
Additivity Over Intervals
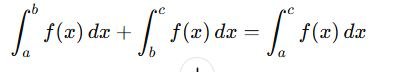
Reversing Limits
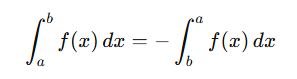
Zero Interval
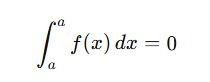
Constant Multiple Rule
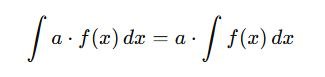
3. Common Integration Formulas
Here are some commonly used integrals:

4. Methods of Integration
1. Substitution Method
Used when the integral contains a composite function.
Example:
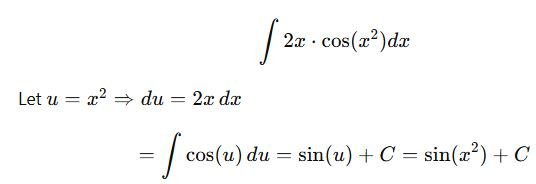
2. Integration by Parts
Based on the product rule for differentiation:
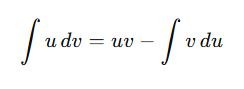
Example:
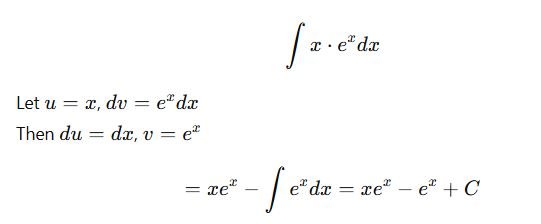
3. Partial Fractions
Used when integrating rational functions.
Example:
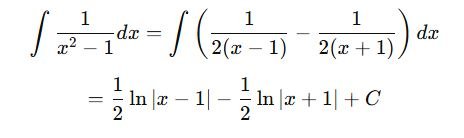
4. Trigonometric Identities
Helpful in simplifying trigonometric integrals.
Example:
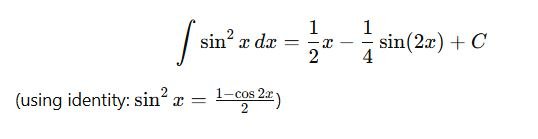
5. Applications of Integration in Daily Life
It is not just theoretical; it’s all around us. Here are several real-world applications:
1. Physics
- Displacement from velocity:
If velocity v(t) is known, then displacement is:
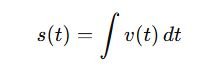
- Work done by a variable force:
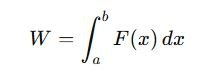
2. Economics
- Consumer and Producer Surplus:
Integration is used to compute surplus areas between demand/supply curves and price levels. - Total Cost or Revenue from marginal functions.
3. Engineering
- The center of Mass and Moment of Inertia are calculated using this over complex bodies.
- Signal processing uses integration to analyze continuous signals.
4. Medicine and Biology
- Drug concentration models often use integration to calculate the total drug exposure (AUC – Area Under Curve).
- Population modeling over time.
5. Architecture and Construction
- Used to determine area, volume, and load distribution in design and structural analysis.
6. Environmental Science
- Pollution modeling: Estimating the total pollutant over time or space.
- Water flow estimation in dams and rivers.
Conclusion
Integration is a cornerstone of calculus with broad and impactful applications in science, engineering, economics, and beyond. Whether calculating the area under a curve or determining how much of a resource is consumed over time, it provides the tools to solve complex real-world problems. By mastering its properties, methods, and applications, students and professionals can better understand how mathematics models and influences the world around us.
Read Also: Understanding Calculus: The Language of Change and Motion
Mastering the (a+b)^2 Formula: Practical Examples and Solutions.
Demystifying Arithmetic Progression: The Essential Maths Sequence.